Biotracing for Dummies
Gary Barker, IFR developed this example. The example is taken from this source
A Bayesian network is a compact model representation used for reasoning when a considerable amount of uncertainty is associated with the information that quantifies a system (i.e., a food chain). Such a model includes steps in the chain and processes along the chain, together with prior probability distributions on these steps and conditional probability distributions describing dependencies. A Bayesian network facilitates inference, i.e., it supports tracing. Figure 1 shows a limited-memory influence diagram representation of the problem domain called SimpleTrace (see [1]).
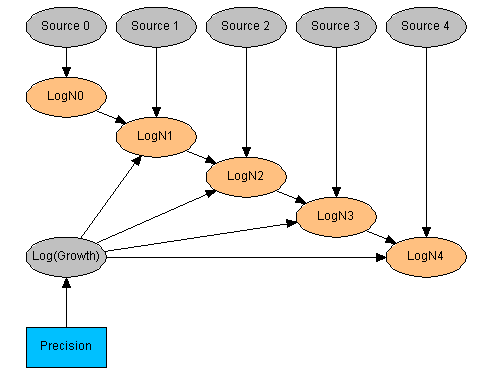
Figure 1: The SimpleTrace network.
The SimpleTrace network represents a finite chain of events with five identified (observable) elements i=0,4. At each stage of the chain an agent has a concentration Ni (The logarithm, LogNi, is the representative random variable). At each stage there is an uncertain source of agent with a fixed concentration 0.1. Boolean variables, Si, quatify the sources - all sources have prior probability 0.005.
Between consecutive elements in the chain finite concentrations of agent grow with an uncertain growth factor, in the range 1 - 100, expressed as log(Ni+1/Ni) ~ Beta(m,m,0,2). (In the network representation concentrations Ni < 0.01 are considered zero - the lowest concentration state acts as a sink). The growth factor is the same for all transitions. A decision node (Precision) can be used to choose m=200,20,1 (High, Medium, Low precision concerning the growth factor).
SimpleTrace illustrates a "biotrace" operation. Observations of the end point concentration, i.e. evidence entered at LogN4, provides posterior belief concerning the sources (source strengths). The ability to identify a source as the origin of observed agents (i.e. "biotrace") depends on the decision concerning the precision of the growth factor.
We have five time-steps in the food chain; every time-step is characterized by a population-distribution of a pathogen (LogN0 to LogN4). At every time-step we have a potential source of contamination (Source 0 to 4). Every population size only depends on the previous population size and on an element of growth. The latter is expressed by the growth factor. We assume that we can only measure the population size at the last time-step.
The measure variable LogN4 has been
discretised into 38 intervals from -3 to 7.25. The intervals are:
([-3;-2[, [-2;-1.75[, [-1.75;-1.5[, ..., [1.25;1.5[, ..., [7;7.25]).
Demonstration of the model
Select Growth Precision
Enter the measured value (possible values are between -3 and 7.25)
Analysis Results
| Possible Source | Probability | Probability (bar view) |
| Source 0: | ||
| Source 1: | ||
| Source 2: | ||
| Source 3: | ||
| Source 4: |
When using the above web form select Growth Precision as High and enter an observation for contamination at the last time-step, Log4N, as 1.35. The information propagation performed by HUGIN updates the beliefs on the initial contamination. It can be seen that the contamination probably occurred at time-step 2. There is a probability of 94.96% that the contamination came from Source 2.
Upload a single case from local disk
This option allows the user to upload data from a HUGIN case file stored on local disk.
Load a case file from local disk: The uploaded file should adhere to the format of HUGIN case files.
Upload a batch of cases from local disk to be processed
This option allows the user to upload a set of cases form a HUGIN data file stored on local disk.
Load a case file from local disk: The uploaded file should adhere to the format of HUGIN data files.